

Informally, an interactive proof is a protocol between two parties in which one party, called the prover, tries to prove a certain fact to the other party, called the verifier. An interactive proof usually takes the form of a challenge-response protocol, in which the prover and the verifier exchange messages and the verifier outputs either "accept" or "reject" at the end of the protocol. Besides their theoretical interests, interactive proofs have found applications in cryptography and computer security such as identification and authentication. In these situations, the fact to be proved is usually related to the prover's identity, e.g., the prover's private key.
The following properties of interactive proofs are quite useful, especially in cryptographic applications:
A typical round in a zero-knowledge proof consists of a "commitment" message from the prover, followed by a challenge from the verifier, and then a response to the challenge from the prover. The protocol may be repeated for many rounds. Based on the prover's responses in all the rounds, the verifier decides whether to accept or reject the proof.
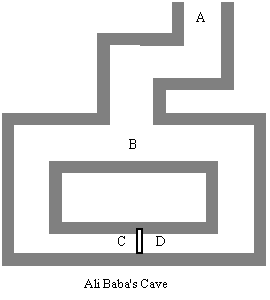
Figure 11. Ali Baba's Cave
Let us consider an intuitive example called Ali Baba's Cave [QG90] (see Figure 11). Alice wants to prove to Bob that she knows the secret words that will open the portal at CD in the cave, but she does not wish to reveal the secret to Bob. In this scenario, Alice's commitment is to go to C or D. A typical round in the proof proceeds as follows: Bob goes to A and waits there while Alice goes to C or D. Bob then goes to B and shouts to ask Alice to appear from either the right side or the left side of the tunnel. If Alice does not know the secret words (e.g., "Open Sesame"), there is only a 50 percent chance that she will come out from the right tunnel. Bob will repeat this round as many times as he desires until he is certain that Alice knows the secret words. No matter how many times that the proof repeats, Bob does not learn the secret words.
There are a number of zero-knowledge protocols in use today as identification schemes. The Fiat-Shamir protocol [FS87] is the first practical zero-knowledge protocol with cryptographic applications and is based on the difficulty of factoring. A more common variation of the Fiat-Shamir protocol is the Feige-Fiat-Shamir scheme [FFS88]. Guillou and Quisquater [GQ88] further improved Fiat-Shamir's protocol in terms of memory requirements and interaction (the number of rounds in the protocol).
Zero-knowledge identification schemes can usually be modified into digital signature schemes (see Question 3 and [FS87]).