

Elliptic curves are mathematical constructions from number theory and algebraic geometry, which in recent years have found numerous applications in cryptography.
Figure 1. Elliptic curve addition.
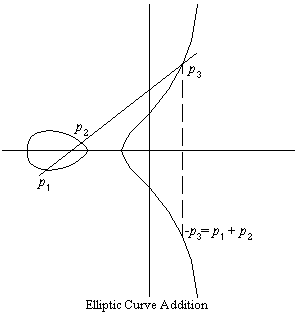
An elliptic curve can be defined over any field (e.g., real, rational, complex). However, elliptic curves used in cryptography are mainly defined over finite fields. An elliptic curve consists of elements (x, y) satisfying the equation
y2 = x3 + ax + b
together with a single element denoted O called the "point at infinity," which can be visualized as the point at the top and bottom of every vertical line. Addition of two points on a elliptic curve is defined according to a set of simple rules (e.g., point p1 plus point p2 is equal to point -p3 in Figure 2). The addition operation in an elliptic curve is the counterpart to modular multiplication in common public-key cryptosystems, and multiple addition is the counterpart to modular exponentiation. Elliptic curves are covered in more recent texts on cryptography, including a informative text by Koblitz [Kob94].