

Blind signature schemes, first introduced by Chaum [Cha83][Cha85], allow a person to get a message signed by another party without revealing any information about the message to the other party.
Chaum demonstrated the implementation of this concept using RSA signatures (see Question 8) as follows: Suppose Alice has a message m that she wishes to have signed by Bob, and she does not want Bob to learn anything about m. Let (n,e) be Bob's public key and (n,d) be his private key. Alice generates a random value r such that gcd(r, n) = 1 and sends
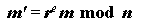
to Bob. The value m' is "blinded" by the random value r, and hence Bob can derive no useful information from it. Bob returns the signed value,
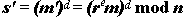
to Alice. Since s'=rmd mod n, Alice can obtain the true signature s of m by computing
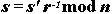
Now Alice's message has a signature she could not have obtained on her own. This signature scheme is secure provided that factoring and root extraction remain difficult. However, regardless of the status of these problems the signature scheme is unconditionally "blind" since r is random. The random r does not allow the signer to learn about the message even if the signer can solve the underlying hard problems.
There are potential problems if Alice can give an arbitrary message to be signed, since this effectively enables her to mount a chosen message attack. One way of thwarting this kind of attack is described in [CFN88].
Blind signatures have numerous uses including timestamping (see Question 108), anonymous access control, and digital cash (see Question 138). Thus it is not surprising there are now numerous variations on the blind signature theme. Further work on blind signatures has been carried out in recent years [FY94] [SPC95].