The discrete logarithm problem applies to groups. Given an element
g in a group G of order t, and another element y
of G, the problem is find x , where 0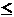 
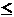x t
- 1, such that y is the result of composing g with itself
x times. The element g can typically generate all the elements
of G or at least a large subset by exponentiating (i.e., applying
the group operation repeatedly) with all the integers from 0 to t
- 1. The element g is called a generator if it can generate all
the elements in the group.
Like the factoring problem, the discrete logarithm problem is believed to be difficult and also to be the hard direction of a one-way function. For this reason, it has been the basis of several public-key cryptosystems, including the ElGamal system and DSS (see Question 29 and Question 26). The discrete logarithm problem bears the same relation to these systems as factoring does to RSA: the security of these systems rests on the assumption that discrete logarithms are difficult to compute.
The discrete logarithm problem has received much attention in recent
years; descriptions of some of the most efficient algorithms for discrete
logarithms over finite fields can be found in
[Odl84]
[LL90]
[COS86]
[Gor93]
[GM93].
The best discrete logarithm problems have expected running times similar
to those of the best factoring algorithms. Rivest
[Riv92a] has analyzed
the expected time to solve the discrete logarithm problem both in terms
of computing power and cost. The discrete logarithm problem appears to
be much harder over arbitrary groups than over finite fields; this is the
motivation for cryptosystems based on elliptic curves (see
Question 31). In general, the running time for computing discrete logarithms
in arbitrary groups is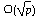 
, where p is the order of the group
[Pol74].