Secret sharing schemes were discovered independently by Blakley [Bla79] and Shamir [Sha79]. The motivation for secret sharing is secure key management. In some situations, there is usually one secret key that provides access to many important files. If such a key is lost (e.g., the person who knows the key becomes unavailable, or the computer which stores the key is destroyed), then all the important files become inaccessible. The basic idea in secret sharing is to divide the secret key into pieces and distribute the pieces to different persons so that certain subsets of the persons can get together to recover the key.
The general model for secret sharing is called an m-out-of-n scheme
(or (m,n)-threshold scheme) for integers 1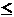 
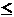m n. In
the scheme, there is a sender (or dealer) and n participants.
The sender divides the secret into n parts and gives each participant
one part so that any m parts can be put together to recover the
secret, but any m - 1 parts reveal no information about the secret.
The pieces are usually called shares or shadows. Different
choices for the values of m and n reflect the tradeoff between
security and reliability. A secret sharing scheme is perfect if
any group of at most m - 1 participants (insiders) has no advantage
in guessing the secret over the outsiders.
Both Shamir's scheme (see Question 104) and Blakley's scheme (see Question 105) are m-out-of-n secret sharing schemes. They represent two different ways of constructing such schemes, based on which more advanced secret sharing schemes can be designed. For further information on secret sharing schemes, see [Sim92].