

Shamir's secret sharing scheme [Sha79] is an interpolating scheme based on polynomial interpolation. An (m - 1)-degree polynomial over the finite field GF(q)
F(x) = a0 + a1x + ... + am - 1 xm-1
is constructed such that the coefficient a0 is the secret and all other coefficients are random elements in the field. (The field is known to all participants.) Each of the n shares is a point (xi, yi) on the curve defined by the polynomial, where xi not equal to 0. Given any m shares, the polynomial is uniquely determined and hence the secret a0 can be computed. However, given m - 1 or fewer shares, the secret can be any element in the field. Therefore, Shamir's scheme is a perfect secret sharing scheme (see Question 103).
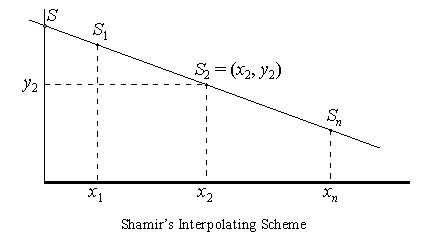
Figure 9. Shamir's secret sharing scheme
A special case where m = 2 (i.e., two shares are required for retrieval of the secret) is given in Figure 9. The polynomial is a line and the secret is the point where the line intersects with the y-axis. Each share is a point on the line. Any two shares (two points) determine the line and hence the secret. With just a single share (point), the line can be any line that passes the point, and hence the secret can be any point on the y-axis.